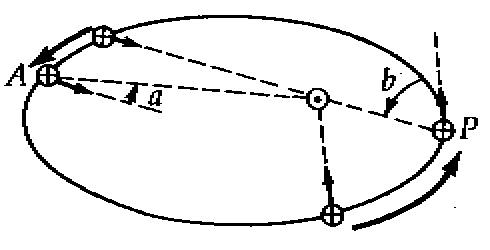
The first of the two factors that can affect the length of the Mean Solar Day is how the Earth revolves around the Sun. The Earth's orbit is slightly elliptical to the Sun. In this exagerated diagram P denotes when the Earth is at perihelion, the closest approach to the Sun, and A when it is furthest away at aphelion. When the Earth is closer to the Sun, such as at perihelion, it will travel faster in it's orbit. In the diagram at perihelion, the Earth has travelled the arc of the arrow in the time it takes to rotate 360 degrees around it's axis and must still revolve through angle b to complete the apparent solar day. Thus the apparent solar day is longer for this time of year. At aphelion the Earth still has the angle a to rotate through at the end of the arc, but since that angle is not as great the time will not be as much for that part of the year.
The other factor is the tilt of the Earth's axis to the Sun. Only the apparent motion of the Sun parallel to the Earth's equator affects the apparent solar day. At each of the equinoxes this factor will be the least, and it has the strongest effect on the solstices of the year. This diagram shows the contrast between the apparent motion of the Sun to the effectual movement for both of these times of the year. On the Equinoxes only the part of the Sun's apparent motion parallel to the Earth's equator, the Effective solar motion, has an effect on the mean solar day. For the solstices, where nearly all of the Sun's apparent motion is along the Earth's equator the effect is stronger.

beemd@astro.wnmu.edu


